PMML 2.0 -- Transformation Dictionary & Derived Values
At various places the mining models use simple functions in order to map user data to values that are easier to use in the specific model. For example, neural networks internally work with numbers, usually in the range from 0 to 1. Numeric input data are mapped to the range [0..1], and categorical fields are mapped to series of 0/1 indicators. Similarly, Naive Bayes models internally map all input data to categorical values.
PMML defines various kinds of simple data transformations:
- Normalization: map values to numbers, the input can be continuous or discrete.
- Discretization: map continuous values to discrete values.
- Value mapping: map discrete values to discrete values.
- Aggregation: summarize or collect groups of values, e.g. compute average.
The corresponding XML elements appear as content of a surrounding markup DerivedField. which provides a common element for the various mappings. They can also appear at several places in the definition of specific models such as neural network or Naive Bayes models. Transformed fields have a name such that statistics and the model can refer to these fields.
The transformations in PMML do not cover the full set of preprocessing functions which may be needed to collect and prepare the data for mining. There are too many varations of preprocessing expressions. Instead, the PMML transformations represent expressions that are created automatically by a mining system. A typical example is the normalization of input values in neural networks. Similarly, a discretization might be constructed by a mining system that computes quantile ranges in order to transform skewed data.
<!ELEMENT TransformationDictionary ( Extension*, DerivedField* ) > <!ENTITY % EXPRESSION "( Constant | FieldRef | NormContinuous | NormDiscrete | Discretize | MapValues | Aggregate)" > <!ELEMENT DerivedField (Extension*, %EXPRESSION; )> <!ATTLIST DerivedField name %FIELD-NAME; #IMPLIED displayName CDATA #IMPLIED > |
DerivedField's in the TransformationDictionary together with DataField's in the DataDictionary must have unique names.
Constant values and references to other fields can be used in expressions which have multiple arguments. Field references are used in clustering models in order to define center coordinates for fields that are not normalized. If a DerivedField is contained in TransformationDictionary, then the name attribute is required. For DerivedFields which are contained inline in models the name is optional.
<!ELEMENT Constant ( Value ) >
<!ELEMENT FieldRef >
<!ATTLIST FieldRef
field %FIELD-NAME; #REQUIRED
>
|
Normalization
The elements for normalization provide a basic framework for mapping input values to specific value ranges, usually the numeric range [0 .. 1]. Normalization is used in neural networks. Similar instances are also used in regression models.
<!ENTITY % NORM-INPUT "( NormContinuous | NormDiscrete )" > <!ELEMENT NormContinuous ( Extension*, LinearNorm* ) > <!ATTLIST NormContinuous field %FIELD-NAME; #REQUIRED > |
NormContinuous: defines how to normalize an input field by piecewise linear interpolation.
field: must refer to a field in the data dictionary.
If LinearNorm is missing then the input field is not normalized.
<!ELEMENT LinearNorm EMPTY >
<!ATTLIST LinearNorm
orig %NUMBER; #REQUIRED
norm %NUMBER; #REQUIRED
>
LinearNorm*: defines a sequence of points for a stepwise linear interpolation function. The sequence must contain at least two elements. To simplify processing, the sequence must be sorted by ascending original values. Within NormContinous the elements LinearNorm must be strictly sorted by acending value of orig. Given two points (a1, b1) and (a2, b2) such that there is no other point (a3, b3) with a1<a3<a2, then the normalized value is
b1+ ( x-a1)/(a2-a1)*(b2-b1) for a1 <= x <= a2.
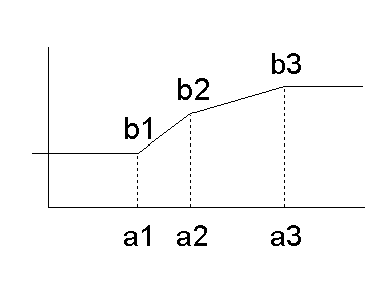
Missing input values are mapped to missing output. If the input value is not within the range [a1..an] then it is treated as an outlier, the specific method for outlier treatment must be provided by the caller. E.g., an outlier could be mapped to a missing value or it could be mapped as the minimal or maximal value.
<!ELEMENT NormDiscrete ( Extension* ) > <!ATTLIST NormDiscrete field %FIELD-NAME; #REQUIRED method ( indicator | thermometer ) #FIXED "indicator" value CDATA #REQUIRED > |
With the indicator method, an element (f, v) defines that the unit has value 1.0 if the value of input field f is v, otherwise it is 0.
The set of NormDiscrete instances which refer to a certain input field define a fan-out function which maps a single input field to a set of normalized fields. Missing input values are mapped to missing output.
PMML 2.0 supports only one kind of discrete normalization, future versions could support other techniques such as thermometer encoding. Thermometer encoding can be used for ordinal values, the output is 1.0 if the value of input field f is greater or equal v, otherwise it is 0.0.
Discretization
Discretization of numerical input fields is a mapping from intervals to strings.
<!ELEMENT Discretize (DiscretizeBin+) >
<!ATTLIST Discretize
field %FIELD-NAME; #REQUIRED
>
<!ELEMENT DiscretizeBin (Interval) >
<!ATTLIST DiscretizeBin
binValue CDATA #REQUIRED
>
|
Two intervals may be mapped to the same categorical value but the mapping for each numerical input value must be unique, i.e., the intervals must be disjoint. The intervals should cover the complete range of input values. If for some value no covering interval is found it is mapped to a missing value. If the input is a missing value the result is a missing value.
A definition such as:
<Discretize field="Profit">
<DiscretizeBin binValue="negative">
<Interval closure="openOpen" rightMargin="0" />
<!-- left margin is -infinity by default -->
</DiscretizeBin>
<DiscretizeBin binValue="positive">
<Interval closure="closedOpen" leftMargin="0" />
<!-- right margin is +infinity by default -->
</DiscretizeBin>
</Discretize>
In SQL this definition corresponds to a CASE expression
CASE When "Profit" <0 Then 'negative' When "Profit" >=0 Then 'positive' End
Map values
Any discrete value can be mapped to any possibly different discrete value by listing the pairs of values. This list is implemented by a Table, so it can be given inline by a sequence of XML markups or by a reference to an external table. The same technique is used for a Hierarchy because the tables can become quite large.<!ELEMENT MapValues (FieldColumnPair+, %TABLE; ) > <!ATTLIST MapValues outputColumn CDATA #REQUIRED defaultValue CDATA #IMPLIED > <!ELEMENT FieldColumnPair () > <!ATTLIST FieldColumnPair field %FIELD-NAME; #REQUIRED column CDATA #REQUIRED > |
Different string values can be mapped to one value but it is an error if the table entries used for matching are not unique. The value mapping may be partial. I.e., if an input value does not match a value in the mapping table, then the result is a missing value. If a defaultValue is given then an input value which has no matching entry in the table is mapped to the default value. The same is true if the input is a missing value.
A definition such as
<MapValues outputColumn="longForm">
<FieldColumnPair field="gender" column="shortForm"/>
<InlineTable><Extension>
<row><shortForm>m</shortForm><longForm>male</longForm>
</row>
<row><shortForm>f</shortForm><longForm>female</longForm>
</row>
</Extension></InlineTable>
</MapValues>
In SQL this definition corresponds to a CASE expression
CASE "gender" When 'm' Then 'male' When 'f' Then 'female' End
An attribute 'defaultValue' would implemented by adding Else SomeDefault.
Aggregations
Association rules and sequences refer to sets of items. These sets can be defined by an aggregation over sets of input records. The records are grouped together by one of the fields and the values in this grouping field partition the sets of records for an aggregation. This corresponds to the conventional aggregation in SQL with a 'GROUP BY' clause.
<!ELEMENT Aggregate ( ) >
<!ATTLIST Aggregate
field %FIELD-NAME; #REQUIRED
function "count | sum | average |
min | max| multiset " #REQUIRED
groupField %FIELD-NAME; #IMPLIED
sqlWhere CDATA #IMPLIED
>
|
A definition such as:
<Aggregate field="item" function="multiset" groupField="transaction"/> |
builds sets of item values; for each transaction, i.e. for each value in the field "transaction" there is one set of items.
